梯度下降(Gradient Descent)

上一篇我們介紹單一變數的斜率，今天我們就進一步探討多個變數的個別斜率，即梯度(Gradient)，並且利用『梯度下降』(Gradient Descent)的原理，計算深度學習模型的權重，有關深度學習模型的求解過程請參考『Day 03：Neural Network 的概念探討』。

簡單的說，深度學習模型的求解過程就是利用正向傳導(Forward Propagation)的過程，求算目標估計值，再利用反向傳導(Backpropagation)，計算梯度，進而調整權重，使成本函數逐漸變變小，重複正向/反向循環，直到成本函數已無顯著改善時，我們就認為已找到最佳的權重值了。有關『梯度下降』(Gradient Descent)的詳細說明，請參考『Day N+1：進一步理解梯度下降』(Gradient Descent)。

單變數求解

計算梯度(Gradient)可利用偏微分(partial differentiation)，對個別變數求一階導數(First Derivative)。以下先以一個變數為例，參考下圖，我們可以沿著切線往下走，步幅的大小由學習率(Learning Rate, lr)控制，逐步往下找到最低點。

import numpy as np
import matplotlib.pyplot as plt

# 目標函數:y=x^2
def func(x): return np.square(x) 

# 目標函數一階導數:dy/dx=2*x
def dfunc(x): return 2 * x 

def GD(x_start, df, epochs, lr):    
    """  梯度下降法。給定起始點與目標函數的一階導函數，求在epochs次反覆運算中x的更新值
        :param x_start: x的起始點    
        :param df: 目標函數的一階導函數    
        :param epochs: 反覆運算週期    
        :param lr: 學習率    
        :return: x在每次反覆運算後的位置（包括起始點），長度為epochs+1    
     """    
    xs = np.zeros(epochs+1)    
    x = x_start    
    xs[0] = x    
    for i in range(epochs):         
        dx = df(x)        
        # v表示x要改變的幅度        
        v = - dx * lr        
        x += v        
        xs[i+1] = x    
    return xs

# Main
# 起始權重
x_start = 5    
# 執行週期數
epochs = 15 
# 學習率   
lr = 0.3   
# 梯度下降法 
# *** Function 可以直接當參數傳遞 ***
x = GD(x_start, dfunc, epochs, lr=lr) 
print (x)

color = list('rgbrgb')    
from numpy import arange
t = arange(-6.0, 6.0, 0.01)
plt.plot(t, func(t), c='y')

line_offset=2 #切線長度
for i in range(5, -1, -1):
    #print(linear_regression([i+0.001, i], [func(i+0.001), func(i)]))
    # 取相近兩個點，畫切線(tangent line)
    z=np.array([i+0.001, i])
    vec=np.vectorize(func)
    cls = np.polyfit(z, vec(z), deg=1)
    p = np.poly1d(cls)
    print(p)
    
    x=np.array([i+line_offset, i-line_offset])
    y=np.array([(i+line_offset)*p[1]+p[0], (i-line_offset)*p[1]+p[0]])
    plt.plot(x, y, c=color[i-1])    

plt.show()

結果如下：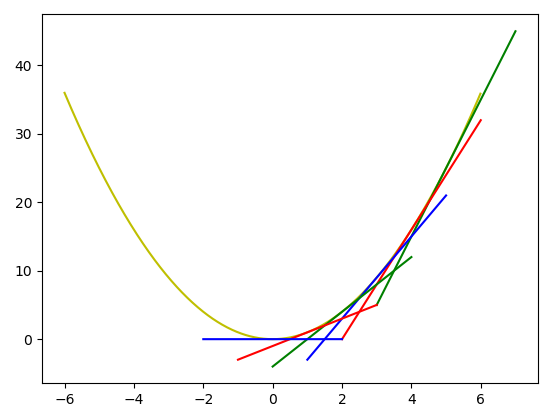

上面程式的 dfunc 函數是偏微分，我們可以使用SymPy自動計算，程式如下，這樣，我們就不用手算了。

from sympy import *
x = symbols('x')
derivative1 = diff(x**2, x)
# 計算某一點(2)的微分值
derivative1.subs(x, 2)

為節省篇幅，上述程式修改後，請參考 github 的 gd_diff.py。

以下，我們就舉兩個完整的範例，均以實際的資料集實作，兩個範例均來自『Python機器學習』一書。

單層感知器求解

假設 y=w0+w1*x，要分別對w0、w1作梯度下降，只要個別對w0、w1偏微分即可，這部份程式可以參考『Python機器學習』的第二章範例程式即可，作者實作了一個感知器(Perceptron)，並以鳶尾花資料集做為測試樣本，我修剪後放在 github 的 ch2_short.ipynb。

重點在權重(w0、w1)的更新，如下：

update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update

多層感知器求解

『Python機器學習』的第十二章更進一步實作多層感知器，並加上『啟動函數』(Activation Function)、『L2正則化』(regularization)，是一個相當完整的範例，有興趣的讀者可參考 ch12.ipynb，本範例以手寫阿拉伯數字資料集做為測試樣本。

結語

透過以上的簡短說明，希望對讀者有一絲絲的幫助，如有謬誤請不吝指正。